Two person zero sum games

• My notes on game theory.



• MATLAB code that made the examples below.


An example:

Pay-off matrix; P = [2 -2; -3 4]

Optimal strategies: for R, (.6364, .3636). For C, (.5454, .4545).

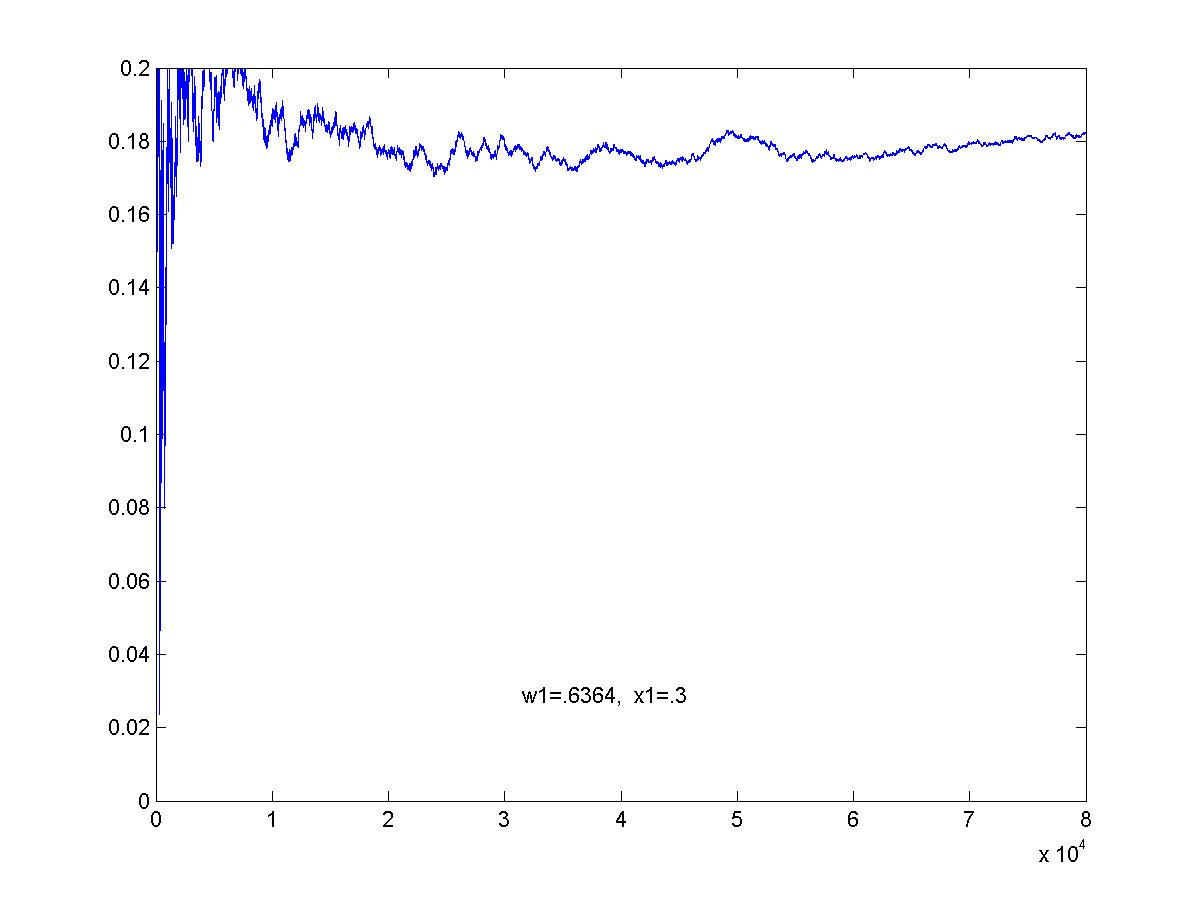
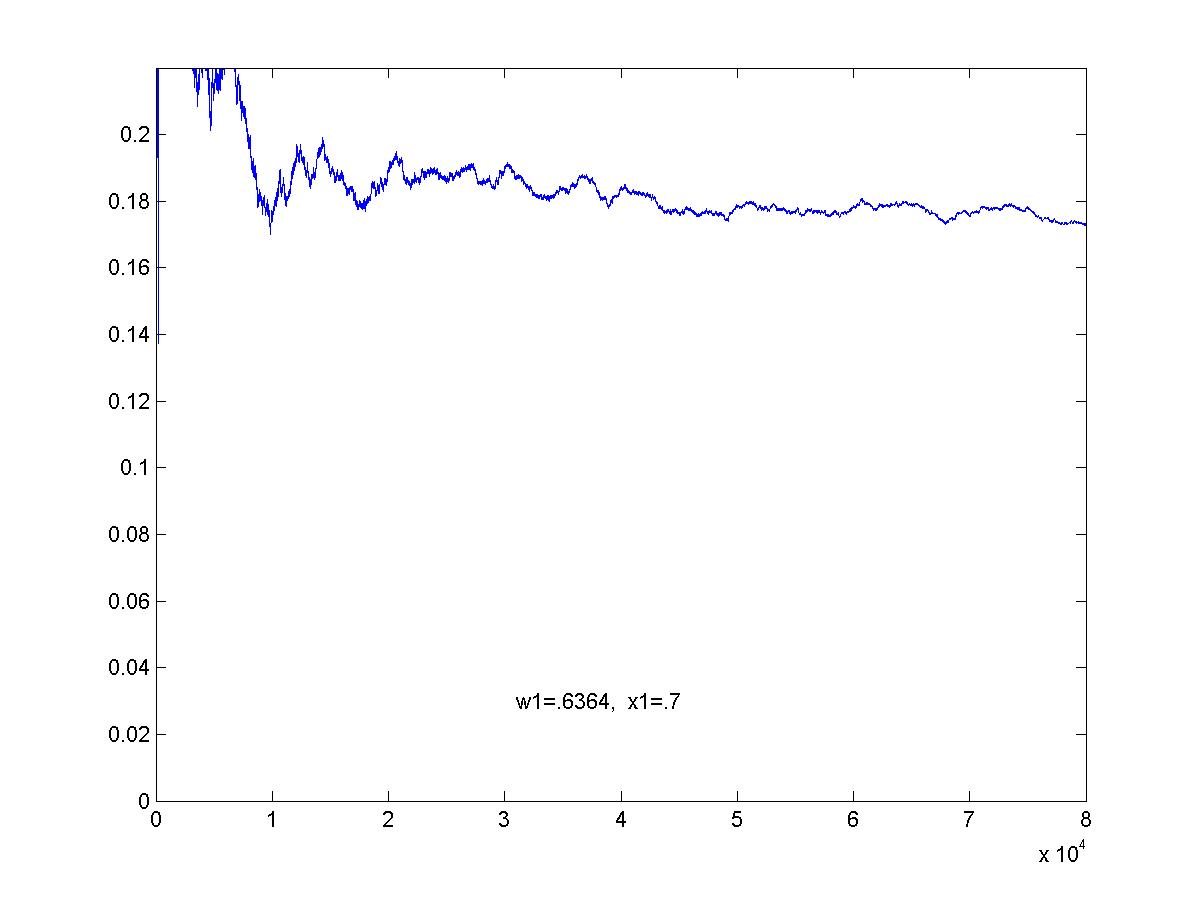
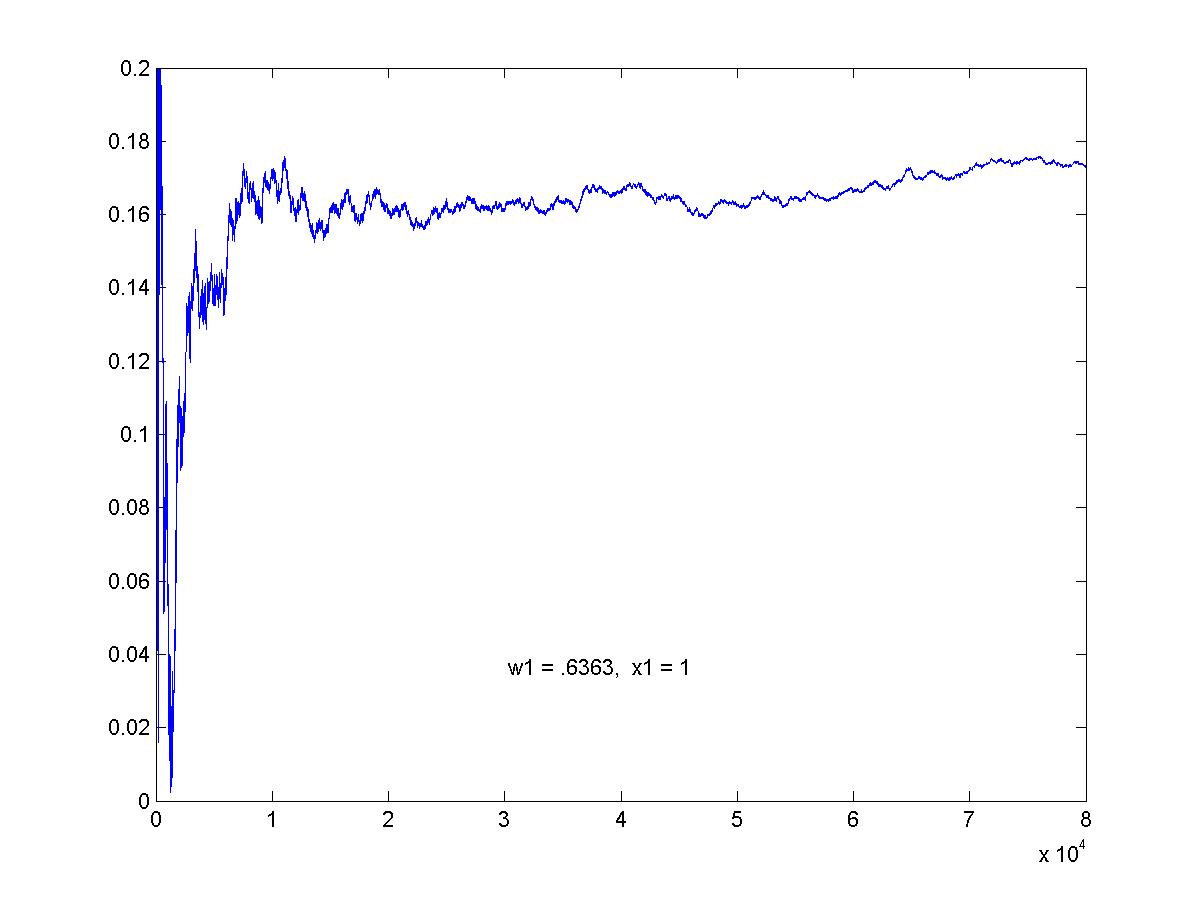
Value of the optimal game: z = .1818.

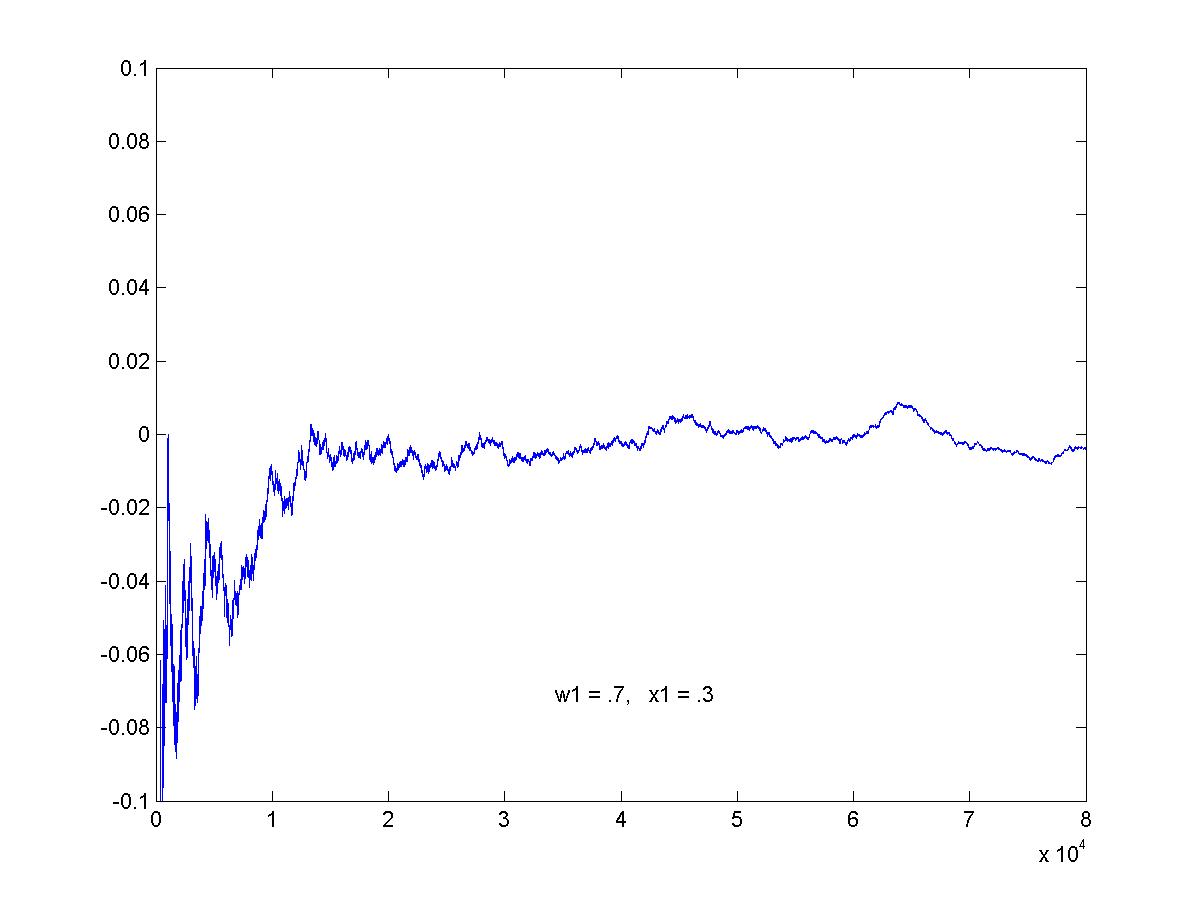
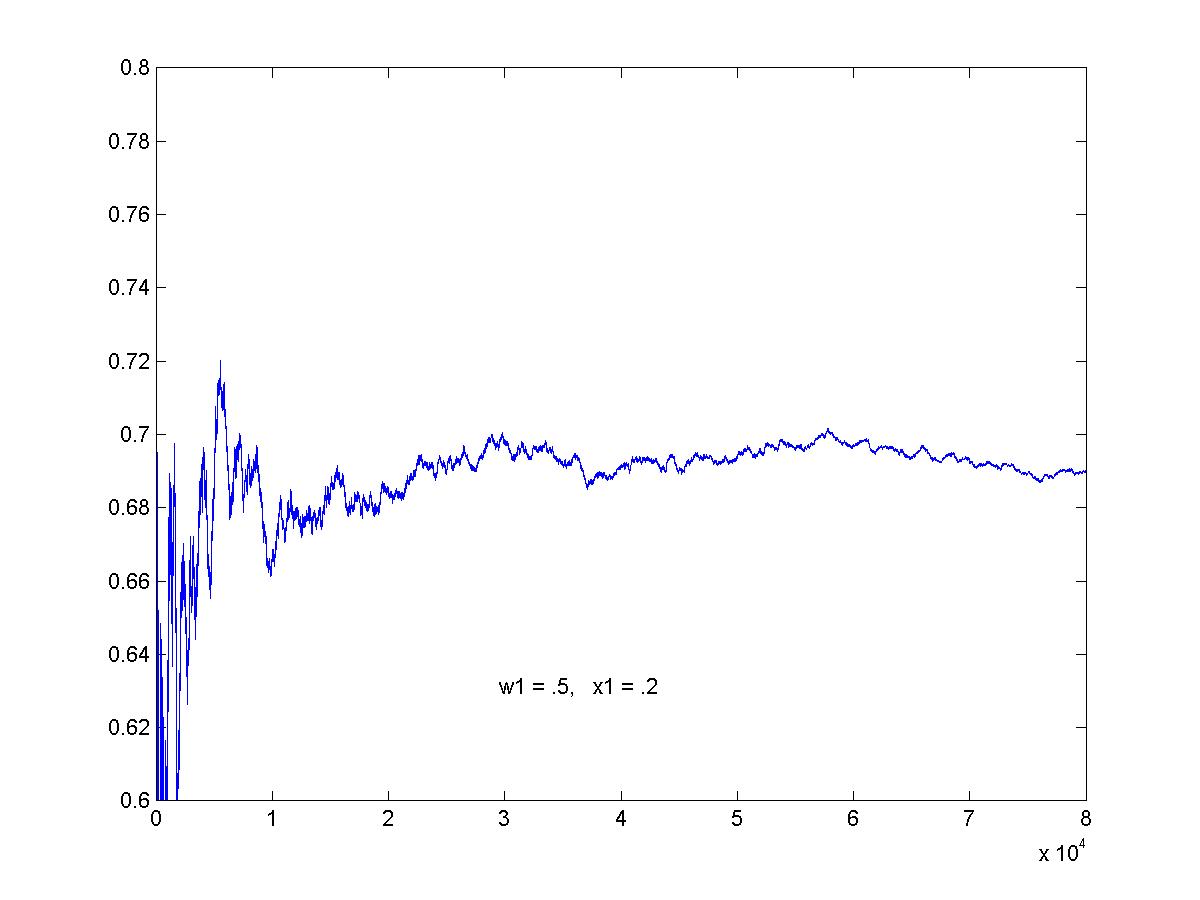
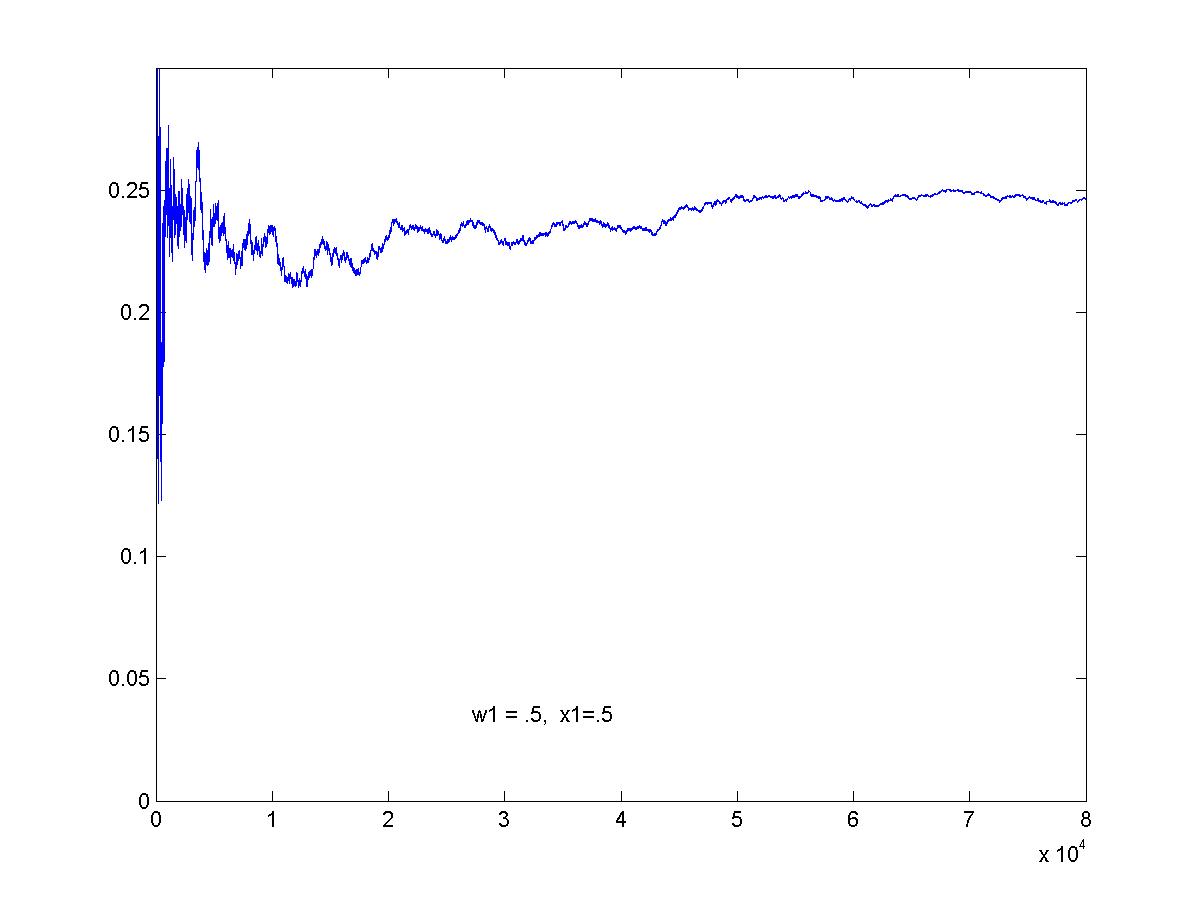
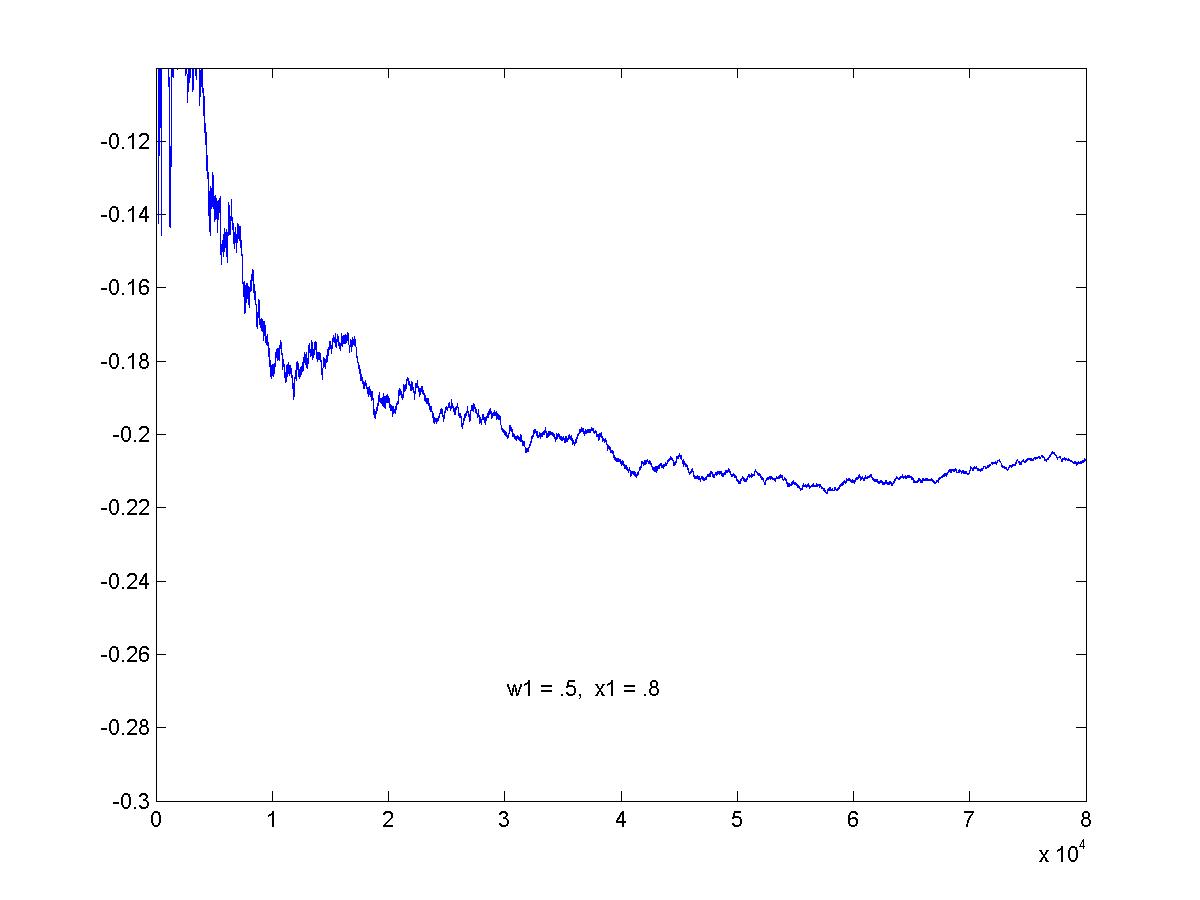
Simulation of optimal game. This is the graph of the average pay-off to R as the game proceeds. The graphs here show 80,000 games (click on image for larger view).



















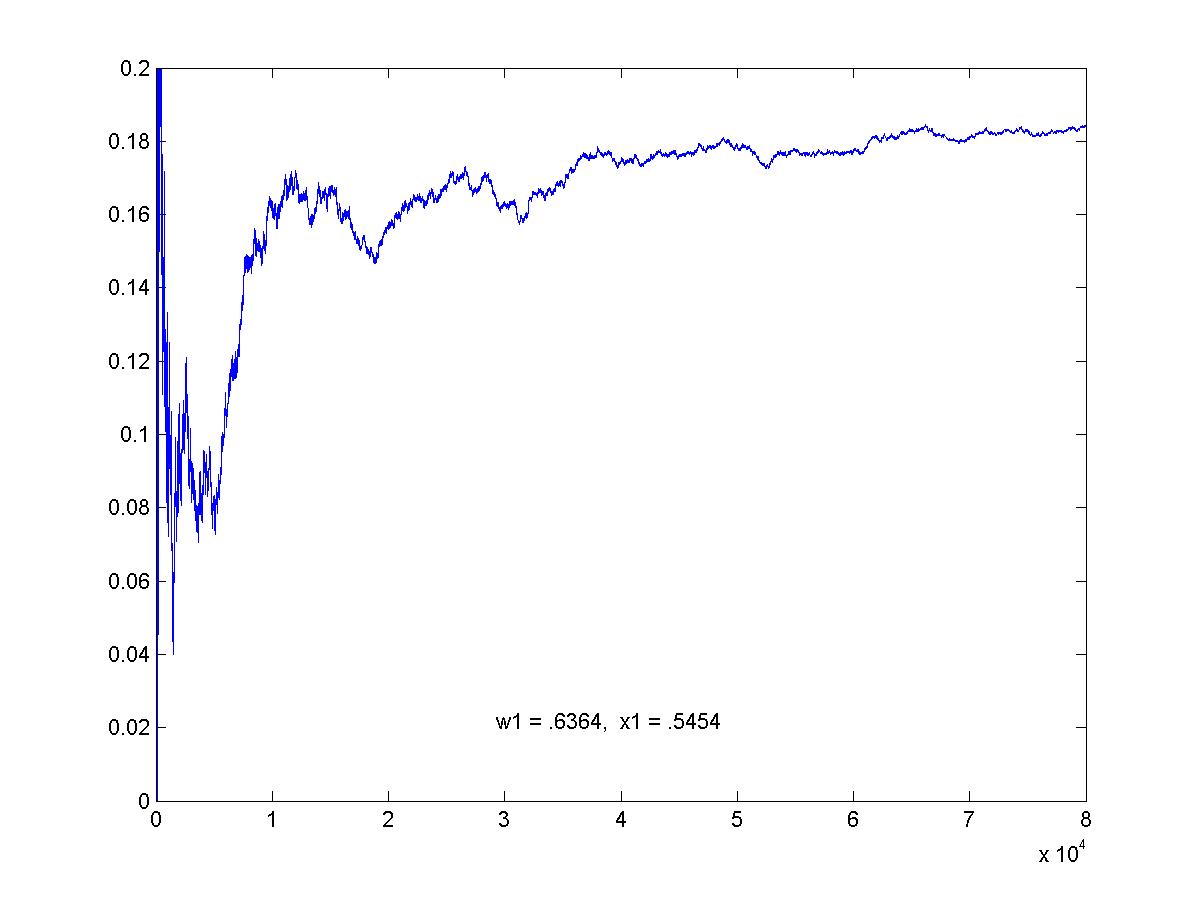
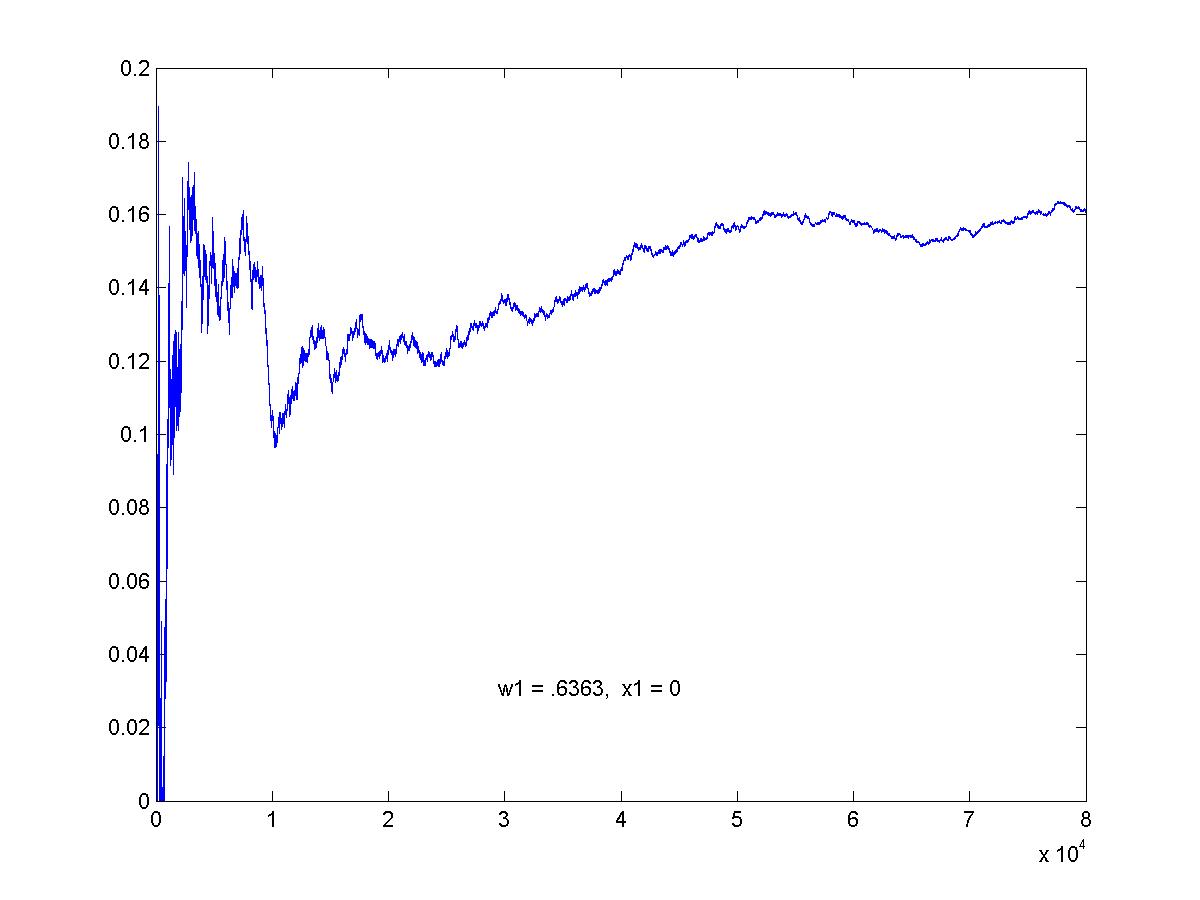
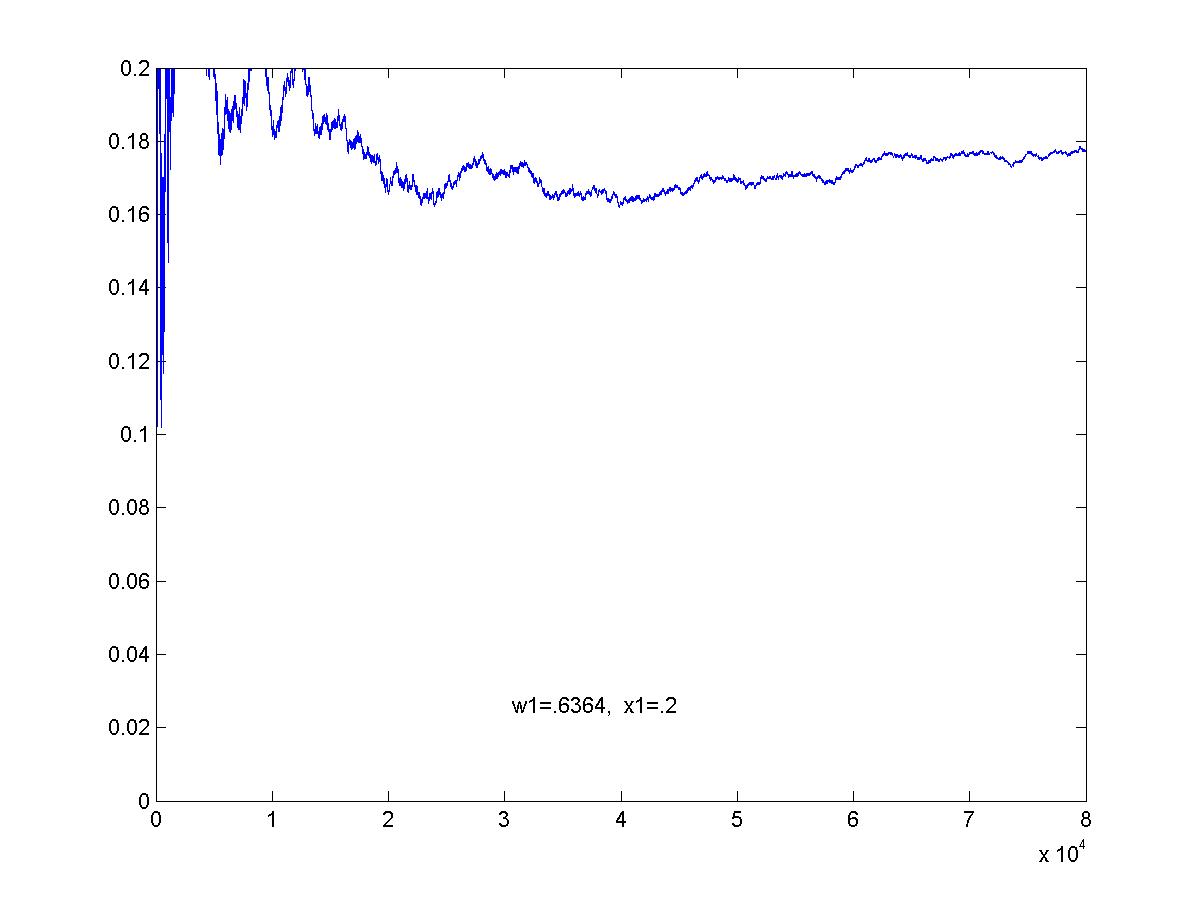
Here, (w1 = .5, x1 = .2).




A sub-optimal game (w1=.5, x1=.5). Here, R gains at the expense of C. Does it seem reasonable to you that the average pay-off in the long run is 0.25?




Here, (w1 = .5, x1 = .8).




Another sub-optimal game (w1=.7, x1=.3). Here, C gains at the expense of R;